Standing waves at the resonant frequency points of an open- or short-circuited transmission line produce unusual effects. When the signal frequency is such that exactly 1/2 wave or somemultiple thereof matches the line's length, the source "sees" the load impedance as it is. The following pair of illustrations shows an open-circuited line operating at 1/2 and 1 wavelength frequencies:
In either case, the line has voltage antinodes at both ends, and current nodes at both ends.Thatis to say, there is maximum voltage and minimum current at either end of the line, which corresponds to the condition of an open circuit. The fact that this condition exists at both endsof the line tells us that the line faithfully reproduces its terminating impedance at the source end,so that the source "sees" an open circuit where it connects to the transmission line, just as if it were directly open-circuited. The same is true if the transmission line is terminated by a short: at signal frequencies corresponding to 1/2 wavelength or some multiple thereof, the source "sees" a short circuit, with minimum voltage and maximum current present at the connection points between source and transmission line:
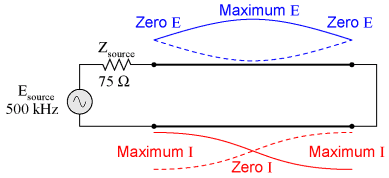
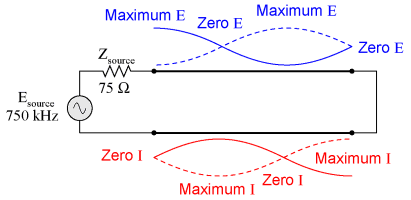
However, if the signal frequency is such that the line resonates at 1/4 wavelength or somemultiple thereof, the source will "see" the exact opposite of the termination impedance. That is, if the line is open-circuited, the source will "see" a short-circuit at the point where it connects tothe line; and if the line is short-circuited, the source will "see" an open circuit:
Line open-circuited; source "sees" a short circuit:
Line short-circuited; source "sees" an open circuit:
At these frequencies, the transmission line is actually functioning as an impedance transformer, transforming an infinite impedance into zero impedance, or vice versa. Of course,this only occurs at resonant points resulting in a standing wave of 1/4 cycle (the line's fundamental, resonant frequency)or some odd multiple (3/4, 5/4, 7/4, 9/4. . .), if the signal frequency is known and unchanging, this phenomenon may be used to match otherwise unmatched impedance to each other. Take for instance the example circuit from the last section where a 75 Ω source connects to a 75 Ω transmission line, terminating in a 100 Ω load impedance.From the numerical figures obtained via SPICE, let's determine what impedance the source"sees" at its end of the transmission line at the line's resonant frequencies:
A simple equation relates line impedance (Z0), load impedance (Zload), and input impedance (Zinput) anunmatched transmission line operating at an odd harmonic of its fundamental frequency:One application of this principle be to match a 300 Ω load to a 75 Ω signal source at a of 50 MHz. All we need to do is calculate the proper transmission line impedance (Z0), and length so exactly 1/4 of a wave will "stand" on the line at a frequency of 50 First, calculating the line impedance: taking the 75 Ω we desire the source to "see" at the source-end the transmission line, and multiplying by the 300 Ω load resistance, we obtain a figure of 22,500. Taking the square root of 22,500 yields 150 Ω for a characteristic line impedance.Now, to calculate the necessaryline length:assuming that our cable has a velocity factor of 0.85, and using a speed-of-light figure of 186,000 miles per second, the velocity of propagation will be 158,100 miles per second. Taking this velocity and dividing by the signal frequency gives us a wavelength of 0.003162 miles, or 16.695 feet. Since we only need one-quarter of this length for the cable to support a quarter-wave, the requisite cable length is 4.1738 Here is a schematic diagram for the circuit, showing node numbers for the SPICE analysis we're about to run:
We can specify the cable length in SPICE in terms of time delay from beginning to end. Since the frequency is50 MHz, the signal period will be the reciprocal of that, or 20 nano-seconds (20 ns). One-quarter of that time(5 ns) will be the time delay of a transmission line one-quarter wavelength long:At a frequency of 50 MHz, our 1-volt signal source drops half of its voltage across the series 75 Ω impedance (v(1,2) ) and the other half of its voltage across the input terminals of the transmission line (v(2) ). This meansthe source "thinks" it is powering a 75 Ω load. The actual load impedance, however, receives a full 1 volt, as indicated by the 1.000 figure at v(3) . With 0.5 volt dropped across 75 Ω, the source is dissipating 3.333 mWof power: the same as dissipated by 1 volt across the 300 Ω load, indicating a perfect match of impedance,according to the Maximum Power Transfer Theorem. The 1/4-wavelength, 150 Ω, transmission linesegment has successfully matched the 300 Ω load to the 75 Ω source.Bear in mind, of course, that this only works for 50 MHz and its odd-numbered harmonics. For any other signal frequency to receive the same benefit of matched impedances, the 150 Ω line would have to lengthened or shortened accordingly so that it was exactly 1/4 wavelength long.Strangely enough, the exact same line can also match a 75 Ω load to a 300 Ω source, demonstrating how this phenomenon of impedance transformation is fundamentally different in principle from that of a conventional,two-winding transformer:Here, we see the 1-volt source voltage equally split between the 300 Ω source impedance (v(1,2) )and the line's input (v(2) ), indicating that the load "appears" as a 300 Ω impedance from the source'sperspective where it connects to the transmission line. This 0.5 volt drop across the source's 300 Ωinternal impedance yields a power figure of 833.33 μW, the same as the 0.25 volts across the 75 Ωload, as indicated by voltage figure v(3) . Once again, the impedance values of source and load have been matched by the transmission line segment.This technique of impedance matching is often used to match the differing impedance values oftransmission line and antenna in radio transmitter systems, because the transmitter's frequency isgenerally well-known and unchanging. The use of an impedance "transformer" 1/4 wavelength inlength provides impedance matching using the shortest conductor length possible.
Review
A transmission line with standing waves may be used to match different impedance values if operated at the correct frequency(ies).
When operated at a frequency corresponding to a standing wave of 1/4-wavelength along the transmission line, the line's characteristic impedance necessary for impedance transformation must be equal to the square root
Standing waves at the resonant frequency points of an open- or short-circuited transmission
line produce unusual effects. When the signal frequency is such that exactly 1/2 wave or some
multiple thereof matches the line's length, the source "sees" the load impedance as it is. The
following pair of illustrations shows an open-circuited line operating at 1/2 and 1 wavelength
frequencies:
In either case, the line has voltage antinodes at both ends, and current nodes at both ends.
Thatis to say, there is maximum voltage and minimum current at either end of the line, which
corresponds to the condition of an open circuit. The fact that this condition exists at both ends
of the line tells us that the line faithfully reproduces its terminating impedance at the source end,
so that the source "sees" an open circuit where it connects to the transmission line, just as if it
were directly open-circuited. The same is true if the transmission line is terminated by a short:
at signal frequencies corresponding to 1/2 wavelength or some multiple thereof, the source "sees"
a short circuit, with minimum voltage and maximum current present at the connection points
between source and transmission line:
However, if the signal frequency is such that the line resonates at 1/4 wavelength or some
multiple thereof, the source will "see" the exact opposite of the termination impedance. That is,
if the line is open-circuited, the source will "see" a short-circuit at the point where it connects to
the line; and if the line is short-circuited, the source will "see" an open circuit:
Line open-circuited; source "sees" a short circuit:
Line short-circuited; source "sees" an open circuit:
At these frequencies, the transmission line is actually functioning as an impedance transformer, transforming an infinite impedance into zero impedance, or vice versa. Of course,this only occurs
at resonant points resulting in a standing wave of 1/4 cycle (the line's fundamental, resonant
frequency)or some odd multiple (3/4, 5/4, 7/4, 9/4. . .), if the signal frequency is known and
unchanging, this phenomenon may be used to match otherwise unmatched impedance to each
other. Take for instance the example circuit from the last section where a 75 Ω source connects
to a 75 Ω transmission line, terminating in a 100 Ω load impedance.From the numerical figures obtained via SPICE, let's determine what impedance the source"sees" at its end of the transmission line at the line's resonant frequencies:
A simple equation relates line impedance (Z0), load impedance (Zload), and input impedance (Zinput) an
unmatched transmission line operating at an odd harmonic of its fundamental frequency:One application of this
principle be to match a 300 Ω load to a 75 Ω signal source at a of 50 MHz. All we need to do is calculate the
proper transmission line impedance (Z0), and length so exactly 1/4 of a wave will "stand" on the line at a
frequency of 50 First, calculating the line impedance: taking the 75 Ω we desire the source to "see" at the
source-end the transmission line, and multiplying by the 300 Ω load resistance, we obtain a figure of 22,500.
Taking the square root of 22,500 yields 150 Ω for a characteristic line impedance.Now, to calculate the necessary
line length:assuming that our cable has a velocity factor of 0.85, and using a speed-of-light figure of 186,000
miles per second, the velocity of propagation will be 158,100 miles per second. Taking this velocity and dividing
by the signal frequency gives us a wavelength of 0.003162 miles, or 16.695 feet. Since we only need one-quarter
of this length for the cable to support a quarter-wave, the requisite cable length is 4.1738 Here is a schematic
diagram for the circuit, showing node numbers for the SPICE analysis we're about to run:
We can specify the cable length in SPICE in terms of time delay from beginning to end. Since the frequency is
50 MHz, the signal period will be the reciprocal of that, or 20 nano-seconds (20 ns). One-quarter of that time
(5 ns) will be the time delay of a transmission line one-quarter wavelength long:
At a frequency of 50 MHz, our 1-volt signal source drops half of its voltage across the series 75 Ω impedance
(v(1,2) ) and the other half of its voltage across the input terminals of the transmission line (v(2) ). This means
the source "thinks" it is powering a 75 Ω load. The actual load impedance, however, receives a full 1 volt,
as indicated by the 1.000 figure at v(3) . With 0.5 volt dropped across 75 Ω, the source is dissipating 3.333 mW
of power: the same as dissipated by 1 volt across the 300 Ω load, indicating a perfect match of impedance,
according to the Maximum Power Transfer Theorem. The 1/4-wavelength, 150 Ω, transmission line
segment has successfully matched the 300 Ω load to the 75 Ω source.Bear in mind, of course, that this only works
for 50 MHz and its odd-numbered harmonics. For any other signal frequency to receive the same benefit of matched impedances, the 150 Ω line would have to lengthened or shortened accordingly so that it was exactly 1/4 wavelength long.Strangely enough, the exact same line can also match a 75 Ω load to a 300 Ω source, demonstrating
how this phenomenon of impedance transformation is fundamentally different in principle from that of a conventional,two-winding transformer:
Here, we see the 1-volt source voltage equally split between the 300 Ω source impedance (v(1,2) )
and the line's input (v(2) ), indicating that the load "appears" as a 300 Ω impedance from the source's
perspective where it connects to the transmission line. This 0.5 volt drop across the source's 300 Ω
internal impedance yields a power figure of 833.33 μW, the same as the 0.25 volts across the 75 Ω
load, as indicated by voltage figure v(3) . Once again, the impedance values of source and load have
been matched by the transmission line segment.
This technique of impedance matching is often used to match the differing impedance values of
transmission line and antenna in radio transmitter systems, because the transmitter's frequency is
generally well-known and unchanging. The use of an impedance "transformer" 1/4 wavelength in
length provides impedance matching using the shortest conductor length possible.
Review
A transmission line with standing waves may be used to match different impedance values if operated
at the correct frequency(ies).
When operated at a frequency corresponding to a standing wave of 1/4-wavelength along the transmission
When operated at a frequency corresponding to a standing wave of 1/4-wavelength along the transmission
line, the line's characteristic impedance necessary for impedance transformation must be equal to the square
root
